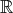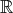10.2 Lieux surface dans ³

La généralistion des lieux de 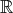² - qui sont la plupart du temps des courbes - sont des surfaces dans 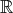³, quand elles peuvent être construites à partir de considérations géométriques (et non à partir d’expressions algébriques), ou e lieux de droites, que l’on nomme courbes géomériques. Etudions les :

10.2.1 Placer un point su un plan

La manière la plus simple de construire un Lieu-surface est de placer un point dans un plan.. Nous allons généraliser à l’espace la construction de la parabole dans le plan : soit PL1 (un plan directeur) et P1 un point (foyer). Cherchons l’enesmble des points P_x équidistants de P1 et PL1.

Construction :

• Construire un point P5 sur PL1
• Construire le plan médiateur de P5 et P1 (sélectionner les deux points, faire ALT-P, puis construire le plan défini par Point et Normale).
• Construire la normale l1 à PL1 passant par P5
• Soit X l’intersection de l1 et PL2.

Maintenant, sélectionner P5 et X, puis faire ALT-O et Paraboloïde apparaît aussitôt.

Le paraboloïde est dynamique, c’est à dire qu’il chenge en focntion de la position des objets de base.

10.2.2 Construire un point dépendant de deux autres points placés sur des droites, des segments ou des cercles.

Pour obtenir une surface, il faut que le pilotage s’effectue selon deux dimensions : un point libre sur un plan, mais également deux points libres sur deux objets (droites, segments, cercles) différents. Un exemple intéressantest la construction d’un paraboloïde hyperbolique qui est l’ensemble des points P_x situés à égale distance de deux droites.

En général, sélectionner un point libre sur une droite, un segment ou un cercle, un second point libre sur le même type d’objet et un point dont la position dépend des deux premiers, et enfin cliquer sur l’icône Lieu-surface.

10.2.3 Construire un cercle, une droite ou un segment dépendant d’un point libre lui même sur un cercle, une droite ou un segment.

Pour créeer un solide de révolution, construire un cercle. Sélectionner un point sur un cercle, un segment ou une droite qui dépend du premier cercle. Cliquer sur l’icône Lieu pour obtenir le Lieu-surface.

De même, il est possible de construire un hyperboloïde à deux nappes que l’on voit au lancement d’Archimedes.

Il est construit de la même manière qu’une hyperbole dans 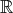². De même, construire un ellipsoïde est analogue à construire une ellipse dans le plan.

En construisant des droites, il est possible de générer des surfaces réglées.