Obwohl Archimedes als Programm für synthetische Geometrie konzipiert wurde, kann man damit durchaus auch Aufgaben der analytischen Geometrie lösen bzw. veranschaulichen.

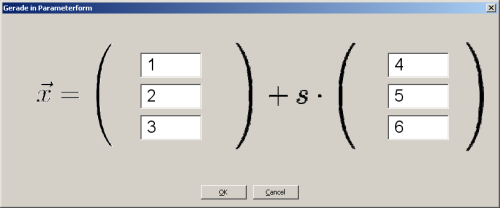
Im obenstehenden Bild wurde die Gerade 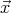 =
=  + s
+ s eingegeben. Archimedes erzeugt
nach Fertigstellung der Eingabe die Gerade, den Stützvektor und den Richtungsvektor.
eingegeben. Archimedes erzeugt
nach Fertigstellung der Eingabe die Gerade, den Stützvektor und den Richtungsvektor.
Statt Zahlen können die Komponenten der Geraden auch Terme enthalten (z.B. Schieberegler für Geradenscharen). Dies muss man dem Programm in der entsprechenden Auswahlbox aber mitteilen.
Wenn man nicht möchte, dass Stützpunkt und Richtungsvektor mit angezeigt werden, so kann man dies mit der Auswahlbox „Hilfsobjekte anzeigen“ einstellen.
Hier können Ebenen in Parameterform, Normalenform und Koordinatenform eingegeben werden.
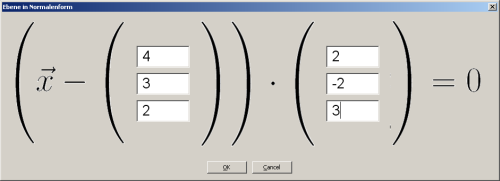
Im obenstehenden Bild wurde die Ebene durch  mit Normalenvektor
mit Normalenvektor 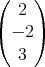 eingegeben. Archimedes erzeugt nach der Eingabe die Ebene, den Stützvektor und den
Normalenvektor.
eingegeben. Archimedes erzeugt nach der Eingabe die Ebene, den Stützvektor und den
Normalenvektor.
Hier kann die Gleichung einer Kugel durch Angabe des Mittelpunktes und des Radius angegeben werden.
Hier kann die Gleichung einer parametrischen Kurve angegeben werden, wie z.B. 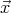 =
= 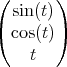 für
eine Schraubenlinie.
für
eine Schraubenlinie.
Dieser Dialog unterstützt bei der Eingabe parametrischer Flächen. Die „Kleinsche Flasche“ aus dem Beispielordner (Unterordner Funktionen) lässt sich als parametrische Fläche erzeugen.
Durch Anwahl dieses Menüpunktes werden die Koordinatenachsen als Geraden erzeugt. Zusätzlich werden der Ursprung und die Einheitsvektoren in die Zeichnung eingefügt.
Die xy-Ebene, die yz-Ebene und die xz-Ebene werden in die Zeichnung eingefügt. Auf den Ebenen wird eine Gittertextur dargestellt, die, so lange die Größe der Ebene nicht verändert wird, maßgenau ist: Eine Gittermasche hat die Länge 1 L. E.
Ein Beispiel für die Verwendung von Archimedes zur Lösung von Schulaufgaben finden Sie unter „Kommentierte Beispiele“, Abschnitt Analytische Geometrie.