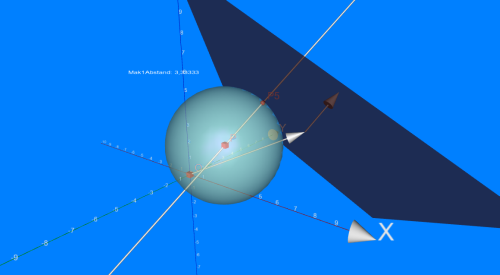
18.2 Géométrie analytique
L’exercice suivant est tiré d’un manuel allemand
Soit E un plan et une famille de droites gp telle que p 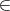
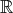 .
.
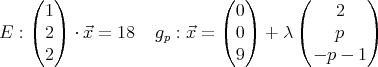
- Trouver une équation de la sphère de centre P(2|1|2) tangente à E. Déterminer les
coordonnées du point de contact.
- Montrer que pour tout p, gp et E sont sécants.
- Pour quelles valeurs de p, les droites sont-elles tangentes à la sphère ?
18.2.1 Solution avec Archimedes
-
- Construire le plan par ’Equations et repère > Plan > Forme générale’ et saisir
x + 2y + 2z = 18.
- Construire le point P par un double-clic-droit puis en ajustant ses coordonnées ou en
utilisant la ligne de commande ’P=(2,1,2)’.
- Construire la perpendiculaire L au plan E passant par P.
- Mesurer la distance de P à L en utilisant un vecteur ou en utilisant la macro ’Distance
- PointPoint’.
- Construire la sphère de centre P passant par L.
La sphère a pour équation 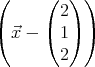 2 = 3
2 = 3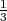 .
.
- Evidemment, Archimède ne prouve pas ce résultat, mais permet de vérifier que l’équation
trouvée semble valable.
- Créer un paramètre ’Outils > Paramètre’, le nommer ’pp’ (car le nom P est déjà
utilisé).
- Gib die Geradengleichung unter "‘Typische Aufgaben - Gerade in Parameterform"’ mit
dem Parameter pp so ein, wie sie in der Aufgabenstellung steht, ersetze dabei lediglich
"‘p"’ durch "‘pp"’. Markiere dabei die Einstellungsbox "‘Ausdruck enthält Terme"’.
- La droite suivra les modifications de valeurs du paramètre.
- On peut trouver expérimentalement que le valeur cherchée du paramètre est 2.We can find
out by trying that the solution for the parameter p is 2, or we could construct the
line (as the parameter is not asked for) and find out the equation by right click -
description.
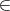
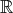 .
.
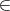
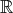 .
.
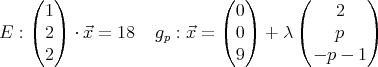
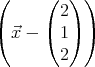 2 = 3
2 = 3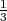 .
.