18.1 Sphère inscrite dans un tétraèdre

Dans 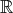² le point de concours des bissectrices d’un triangle est le centre du cercle inscrit. Ce cercle est tangent aux trois côtés du triangle.

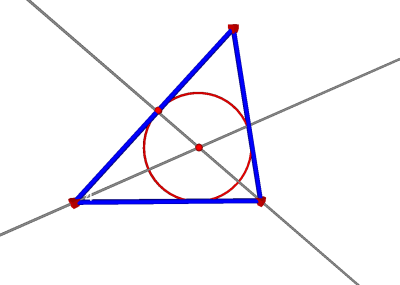
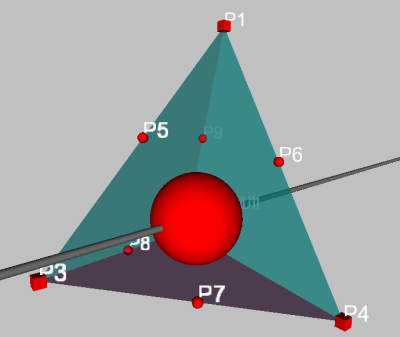
Une construction analogue est possible dans 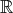³ en construisant la sphère inscrite dans un tétraèdre non régulier.

Par analogie, le point de concours des trois plans bissecteurs est le centre de la sphère inscrite.

Pour construire la sphère, commençons par construire une macro permettant de construire le plan bissecteur.

Il faut donc commencer par définir une orientation afin de pouvoir construire un plan bissecteur d’un angle de deux plans.

On se donne 5 points sur les deux polans : deux sur le premier, un à l’intersection des deux et deux sur le second.

18.1.1 Macro Angle-bissecteur

Si vous préférez utiliser la macro Angle bissecteur, passez ce paragraphe.

Utilisons la construction suivante : soit P1, P2, P3, P4 et P5 des points libres. Soit PLA1 le plan passant par P1, P2 et P3 et PLA2 le plan passant par P3, P4 et P5. On place PLA1 ’à gauche de’ PLA2 ’, P1 sous P2 et P4 sous P5.

Cela assure qu’en utilisant la macro plus tard avec la même orientation, l’angle bissecteur construit sera le même.

Construisons l’intersection des deux plans.

• Construisons PL1
• Construisons PL2
• Construisons L1, droite intersection des deux plans

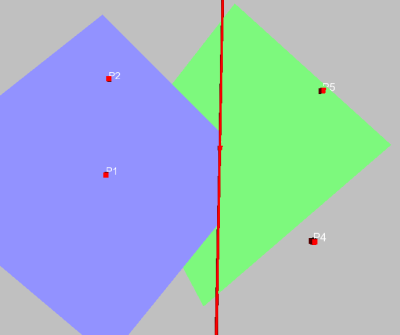
Pour construire le plan bissecteur, il suffit de construire un point équidistant des deux plans. Construisons un cercle centré sur L1 et de rayon non nul quelconque. Par exemple le cercle de centre p3 et passant par P1. Comme plan du cercle, on choisit passant par P3 et perpendiculaire à L1.

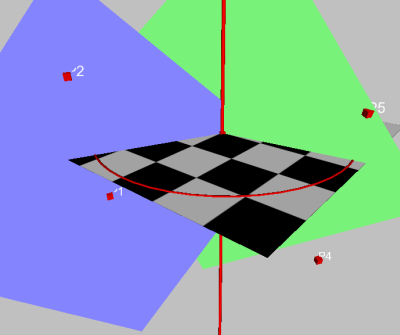
Il suffit maintenant :

• Die Schnittpunkte des Kreises mit den beiden Ebenen bestimmen (z.B. mit dem Schnittbutton)
• On construit le milieu des points trouvés.
• Il nous faut un troisième point pour définir le plan bissecteur. Il suffit d’un point sur L1. Pour ne pas que ce point soit trop proche de P3, ce qui rendraitr la figure instable, on construit la sphère de centre P3 et de rayon P1P4.
• On peut maintenant construire le plan bissecteur.

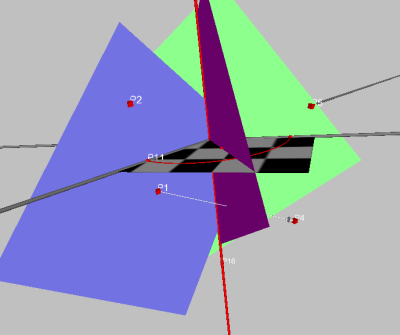
Déplacer les points de base pour vérifier la construction.

On peut maintenant vérifier qu’en changeant les positions relatives des points, la construction conserve l’orientation.

On cache mainenant tous les objets ’intutiles’, on marque les points de base comme objets initiaux et et on enregistre la construction sous ’Planbissecteurdefinipar5points.geosave’, par exemple.

18.1.2 Constuction de la sphère inscrite

Construisons maintenant un tétraèdre à partir de 4 points libres.

Pour utiliser la macro, il y a un petit problème car deux faces n’ont pas un mais deux points en commun ! Nous n’avons donc pas de points en nombre suffisant pour apliquer la macro... ⁷

Il suffit de construire le milieu des faces pour résoudre le problème :

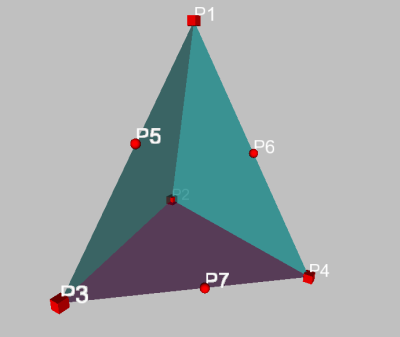
On sélectionne maintenant les points dans l’ordre pour obtenir le premier plan bissecteur :

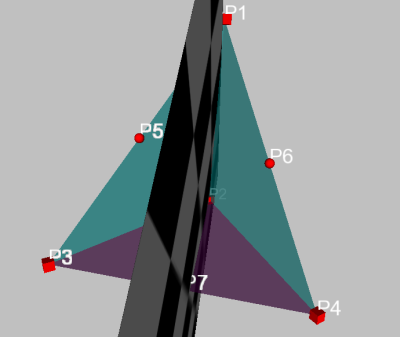
Jetzt muss man nur noch drei weitere Winkelhalbierende konstruieren und dann alle drei markieren, um den Schnittpunkt zu erhalten. Dann fällt man das Lot von diesem Schnittpunkt auf eine der Dreiecksseiten (z.B. durch Markieren des Punktes und des Dreiecks und Drücken des Normalenbuttons im kleinen Toolbar) und hat nun Mittel- und Randpunkt der Inkugel :