4.7 Equations et repère

Si Archimède a été conçu pour la géométrie non analytique, il peut également permettre de traiter des questions analytiques.

4.7.1 Droite sous forme paramétrique

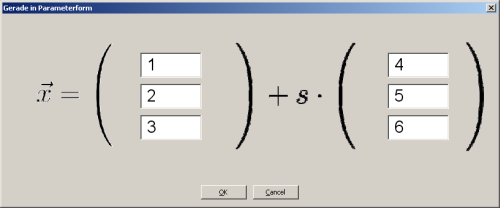
Dans la figure ci-dessous la droite = + s saisie. Archimedes construit la droite, ’le vecteur de position’ et le vecteur directeur indiqués dans l’équation.

Statt Zahlen können die Komponenten der Geraden auch Terme enthalten (z.B. Schieberegler für Geradenscharen). Dies muss man dem Programm in der entsprechenden Auswahlbox aber mitteilen.

Wenn man nicht möchte, dass Stützpunkt und Richtungsvektor mit angezeigt werden, so kann man dies mit der Auswahlbox "‘Hilfsobjekte anzeigen"’ einstellen.

4.7.2 Plan

Donne accès aux équations de plans sous formes paramétrique, normal ou cartésienne.

Illustration d’un plan passant par et de vecteur normal

4.7.3 Sphère

La sphère est définie par les coordonnées de son centre et son rayon.

4.7.4 Courbe paramétrée

Exemple d’une courbe paramétrée : = pour une hélice.

4.7.5 Surface paramétrée

Permet de construire une surface à partir d’une équation paramétrique. Par exemple, la bouteille de Klein.

4.7.6 Axes de coordonnées

Construit les axes de coordonnées, les vecteurs unitaires et l’origine.

4.7.7 Plans de base

Affiche les plans de base muni d’une grille unité.

Exemple d’utilisation d’Archimède dans la section ’Exemples commentés’, subsection Géométrie analytique.