2 Erste Schritte

2.1 Tutorials

Arbeiten Sie alle Tutorien unter „Hilfe - Tutorien“ in der gegebenen Reihenfolge durch.

2.2 Erstellen eines Würfels

An einer Beispielkonstruktion werden wichtige Funktionen des Programms erklärt:

Hier gibt es grundsätzlich zwei Möglichkeiten: Man kann den Würfel konstruieren, oder man kann einfach die Koordinaten der Eckpunkte festlegen. Die zweite Möglichkeit ist zunächst die einfachere:

• Erstelle acht freie Punkte durch achtmaliges Doppelrechtsklicken in die Zeichnung.
• Setze die Koordinaten der Punkte durch Rechtsklick - Einstellungen auf den Punktnamen links in der Liste auf (0, 0, 0), (5, 0, 0), (0, 5, 0), (5, 5, 0), (0, 0, 5, (5, 0, 5), (0, 5, 5), (5, 5, 5). Hier mit der rechten Maustaste klicken:

  

  Hier die Koordinaten eintragen und OK drücken:

  

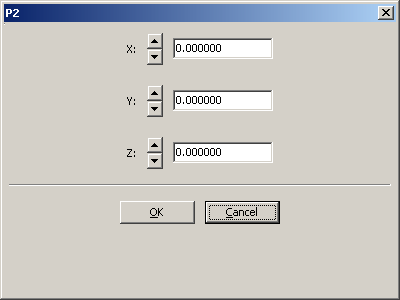
  So sollte es aussehen:

  

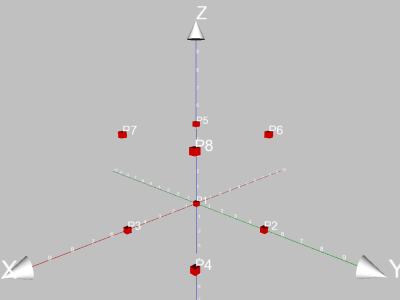
  Tipp: In der Eingabebox für die Punkte kann man gut mit der TABULATORTASTE navigieren.

• Alternativ können die Punkte in der Eingabezeile auch direkt eingegeben werden. Die Eingabe würde dann „A=(0,0,0)“, „B=(5,0,0)“ usw. lauten.
• Nun müssen die Seitenflächen konstruiert werden. Diese sind Quadrate, und können daher als Parallelogramme gezeichnet werden ¹ . Bei einem Parallelogramm müssen drei Ecken markiert werden, die vierte wird dann von dem Programm errechnet. Die Reihenfolge ist wichtig: Der mittlere Punkt ist der Scheitelpunkt des Winkels zwischen den beiden äußeren Punkten. Beispiel: Markiert man die Punkte in der Reihenfolge P2, P1, P3, so erhält man das folgende Parallelogramm:

  

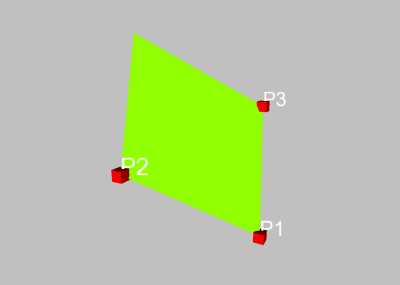
  Wählt man hingegen die Reihenfolge P1, P2, P3, so erhält man dieses Parallelogramm:

  

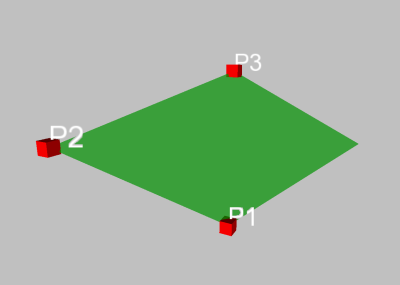
• Der fertige Würfel sieht dann ungefähr so aus:

  

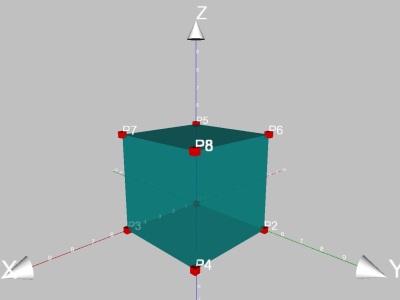
  Jetzt kann man den Würfel noch verschönern, indem man im Kontextmenü der Parallelogramme (Rechtsklick in der Zeichnung) die Farben ändert.

  Wenn man im Menü Extras - Einstellungen - Ansicht - „Zeige Knopfleiste“ die Knopfleiste sichtbar gemacht hat, kann man mehrere Farben gleichzeitig ändern: Wählt man mehrere Objekte aus (z.B. mit SHIFT-Klick in der Zeichnung), dann kann man durch Drücken auf den Schalter „Farbe“ die Farbe aller gewählten Objekte ändern.

  Gleichzeitig kann man auch noch die Transparenz der Flächen einstellen. Dies geschieht auch im Kontextmenü oder mit der Einstellbox „Dichte“ in der Knopfleiste zwischen Zeichnung und Objektbox.

  Alternativ kann man die Seitenflächen des Würfels zu einer Gruppe zusammen fassen (Flächen markieren, anschließend Extras - Gruppieren) und die Farbe für das Gruppenobjekt einstellen.

  Dann könnte der Würfel zum Schluss so aussehen:

  

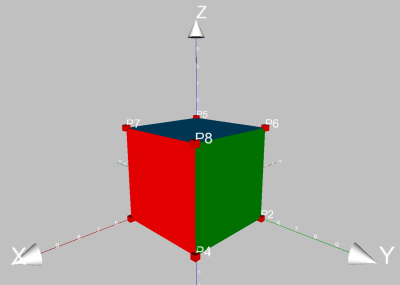
2.3 Konstruktion einer Pyramide

Im letzten Abschnitt wurde ein Würfel durch Angabe seiner Eckpunkte erstellt. Er wurde aber nicht im strengen Sinne „konstruiert“. Wenn man an einem der Eckpunkte ziehen würde, würde der Würfel „auseinanderfallen“.

Daher soll im folgenden Abschnitt eine „richtige“ Pyramide konstruiert werden, genauer: Ein regelmäßiges Tetraeder.

Grober Konstruktionsplan:

• Konstruktion eines gleichseitigen Dreiecks als Grundfläche
• Konstruktion des Mittelpunktes des Dreiecks
• Konstruktion der Pyramidenspitze

Um ein gleichseitiges Dreieck konstruieren zu können, muss man eine Konstruktion „in der Ebene“ durchführen. Daher ist es günstig, zunächst eine Basisebene zu konstruieren. Hierfür kann man z.B. die x-y-Ebene nehmen:

• Erstelle drei freie Punkte und setze sie auf die Koordinaten (0, 0, 0), (1, 0, 0), (0, 1, 0).
• Erstelle eine Ebene durch die drei Punkte durch Markieren der Punkte und anschließendes Klicken auf das Ebenensymbol.
• Damit die Ebene nicht mehr „verstellt“ werden kann, ist es sinnvoll, die drei Basispunkte zu verstecken. Wichtig: Nicht (!) löschen, sonst wird die Ebene, die ja von den Punkten abhängt, gleich mitgelöscht! Alternativ ist es möglich, diese Punkte im Kontextmenü „Einstellungen“ zu fixieren.

Das Ergebnis sollte ungefähr so aussehen:

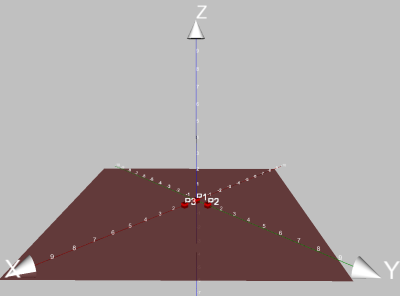
Nun dreht man durch Ziehen mit der linken Maustaste (dabei nicht auf ein Objekt zeigen! Also „ins Blaue“ klicken oder gleichzeitig Alt drücken!) das Koordinatensystem so, dass man ungefähr auf die Ebene draufschaut, damit man besser „in der Ebene“ konstruieren kann.

Jetzt braucht man zwei Punkte in der Ebene, die dann die ersten zwei Ecken des gleichseitigen Dreiecks darstellen. Dazu markiert man die Ebene (durch Klick auf die Ebene in der Zeichnung oder im Objektbaum) und wählt dann den Knopf „Punkt“. Andere Möglichkeit: Wenn eine Ebene markiert ist, erzeugt ein Doppelrechtsklick in der Zeichnung einen Punkt auf der Ebene in der Nähe des Mauszeigers. Hierbei Alt drücken, sonst erscheint das Kontextmenü der Ebene. Dritte Möglichkeit: Man markiert die Ebene und drückt dann Alt - P für Punkt.

Jetzt kann man die Punkte noch zurechtziehen, und sollte in etwa das folgende Bild erhalten:

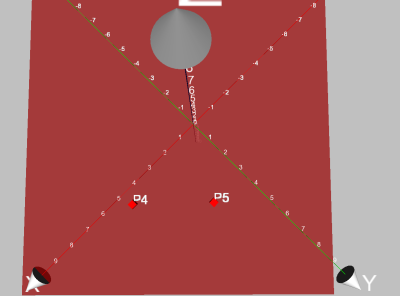
Nun muss man sich überlegen, wie man ein gleichseitiges Dreieck konstruiert: Man zeichnet Kreise um P1 mit Radius |P1P2| und um P2 mit gleichem Radius, der Schnittpunkt liefert den fehlenden Punkt des Dreiecks.

Im Gegensatz zu Konstruktionen in der Ebene reichen zwei Punkte aber nicht aus, um einen Kreis festzulegen. Wenn man P1 und P2 markiert und auf „Kreis“ drückt, erscheint kein Kreis, sondern ein Pop-up Menü. Man muss dem Programm also noch mitteilen, in welcher Ebene der Kreis liegen soll. Und tatsächlich: Wenn man noch zusätzlich die Ebene auswählt, lässt sich direkt ein Kreis konstruieren. Oder man hat im Pop-up Menü „Kreis aus Mittelpunkt, Randpunkt und Kreisebene“ gewählt und dann die entsprechenden Objekte angewählt.

Zeichnet man noch den anderen Kreis, sollte man das folgende Bild erhalten:

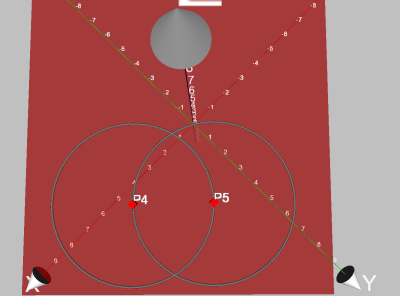
Wenn man nun die beiden Kreise auswählt, werden über den Knopf „Punkt“ (oder über Alt-P) die Schnittpunkte konstruiert.

Den einen der beiden Schnittpunkte kann man getrost löschen, für das gleichseitige Dreieck genügt ein einziger. Außerdem sollte man vielleicht die Kreise verstecken, denn auch diese werden nicht benötigt.

Nun kann man die Punkte durch Strecken verbinden. Besonders schnell geht das, wenn man alle drei Punkte markiert und dann auf Strecke drückt, es entsteht ein geschlossener Streckenzug. ²

Nun sollte man den Mittelpunkt des Dreiecks konstruieren. Da es sich um ein gleichseitiges Dreieck handelt, gibt es hier jetzt verschiedene Möglichkeiten. Die leichteste:

• Zwei Eckpunkte markieren, Punkt drücken, man erhält den Mittelpunkt der beiden Punkte.
• Anschließend verbindet man den Mittelpunkt mit dem gegenüberliegenden Punkt zu einer Seitenhalbierenden. Macht man dies zwei mal, so erhält man den Mittelpunkt des Dreiecks:

  

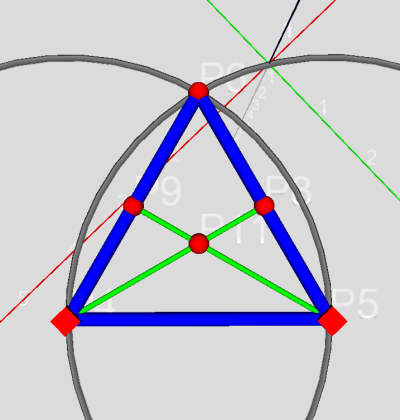
Nun hat man für den noch fehlenden Eckpunkt - die Pyramidenspitze - zwei Bedingungen:

1. Die Spitze ist von den anderen Ecken genau so weit entfernt wie diese voneinander.
2. Die Spitze liegt auf der Normalen zur Basisebene durch den vorher konstruierten Mittelpunkt des Basisdreiecks.

Die zweite Bedingung lässt sich visualisieren, indem man den Mittelpunkt und die Basisebene markiert und anschließend auf „Gerade“ klickt - schon hat man die gesuchte Normale. Irgendwo auf der Normalen muss die Spitze liegen ³.

Die erste Bedingung muss man präzisieren: Von P4 aus gesehen liegen alle Punkte, die gleich weit von P4 entfernt sind wie P5, auf der Kugel um P4 mit Radius |P4 P5|. Also wählt man einfach P4 und P5 aus und lässt die Kugel zeichnen.

Die gesuchte Pyramidenspitze ist dann der Schnittpunkt der Kugel mit der Normalen, den man durch Markieren der beiden fraglichen Objekte leicht konstruieren kann.

Anschließend versteckt man alle unnötigen Objekte, zeichnet die Seitenflächen, koloriert diese hübsch und erhält:

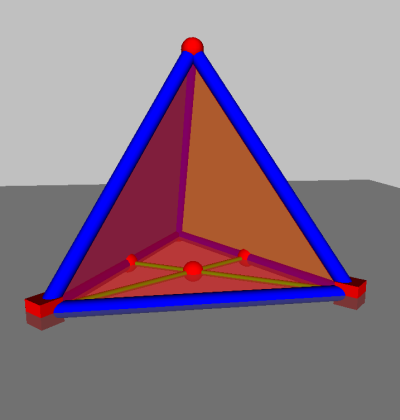
2.3.1 Anbringen einer Textur

Der rein geometrisch Interessierte kann den folgenden, mehr ästhetisch angelegten Abschnitt bedenkenlos überspringen.

Gibt man bei der Google-Bildersuche das Wort „Pyramide“ ein, so erhält man verschiedene Darstellungen der Pyramiden von Gizeh (und einige andere).

Eines der Bilder ermöglicht den freien Blick auf eine der Pyramiden:

Dieses Bild kann man nun auf die Dreiecke des Tetraeders legen. Folgende Schritte sind nötig:

• Bild irgendwo speichern (Rechtsklick auf das Bild, Grafik speichern unter)
• In der Zeichnung im Kontextmenü des Dreiecks „Farbe und Textur“ wählen, dort den Karteireiter Textur anklicken
• Auf „Textur wählen“ klicken
• Das Bild dort auf der Festplatte anwählen, wo man es vorher gespeichert hatte

Falls man seine Konstruktion vorher noch nicht gespeichert hatte, kommt nun eine Fehlermeldung: Archimedes Geo3D kopiert alle Texturen in das Verzeichnis, in dem sich die Konstruktion befindet. Dies dient dazu, zu ermöglichen, die Konstruktion (zusammen mit den Texturen) später auch von einem anderen Ort aus lesen zu können (vermeiden absoluter Dateinamen). Wenn die Konstruktion aber noch nicht gespeichert wurde, weiß Archimedes Geo3D nicht, wohin mit der Textur.

Falls sich eine Textur gleichen Namens bereits im richtigen Verzeichnis befindet, wird man gefragt, ob man diese überschreiben möchte oder nicht.

Wenn man alles richtig gemacht hat, sieht die Dreiecksseite jetzt ungefähr so aus:

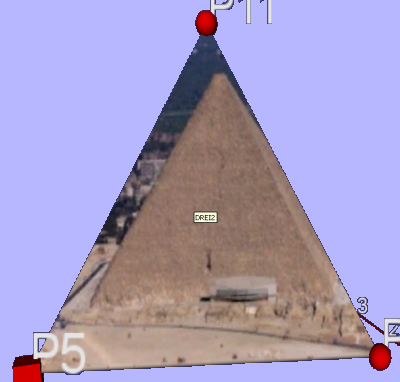
Wenn sie nicht so aussieht, könnte das an folgendem liegen:

• Die Grundfarbe einer Dreiecksseite mit Textur sollte weiß und nicht transparent sein, sonst ist die Textur undeutlich
• Der erste Punkt, der bei der Konstruktion des Dreiecks markiert worden war, bildet die linke untere Ecke der Textur. Ist die Textur verkehrt herum, liegt es daran. Dies lässt sich aber noch ändern (z.B. über „Koordinaten drehen“ im Texturdialog“)

Nun möchte man aber, dass nur die eigentliche Pyramidenseite abgebildet wird.

Dazu bewegt man im Textur-Karteireiter die weißen Punkte im Bild.

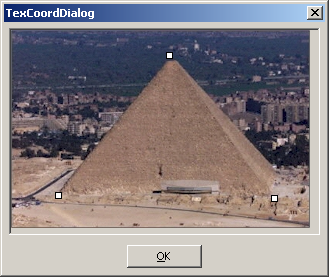
Anschließend drückt man OK.

Hinweis: Die Darstellung der Textur ändert sich in Echtzeit auf dem Dreieck. Es ist daher ratsam, den Dialog so zu positionieren, dass man das Dreieck sieht und das Ergebnis direkt überprüfen kann.

So kann man sich seine eigene Pyramide bauen, und hoffen, dass sich die Ägyptischen Baumeister nicht aus ihren Gruften erheben: Immerhin waren die großen Pyramiden natürlich keine Tetraeder, sondern besaßen eine quadratische Grundfläche...

2.4 Übungsvorschlag

Mit den erworbenen Kenntnissen sollte man in der Lage sein, einen Würfel zu konstruieren. Dieser sollte sich dann nicht mehr „zerreißen“ lassen, sondern das Ändern der Größe über zwei Eckpunkte ermöglichen.