15 Measure and calculate

The most important function of the menu ’measure and calculate’ is the ability to enter expressions.

• The objects you can calculate with are numbers, vectors and points. Numbers can be entered directly or be the result of another expressions. Vectors can be vectors from the scene or results of expressions, too. Vectors can be entered using the command ’vec(x,y,z)’. If you enter the name of a point in an expression, the position vector of that point will be used. You can add points this way, which might be ’unmathematical’, but practical sometimes.
• The usual operators +, -, *, /,ˆare defined. For vectors V1ˆV2 means the cross-product, V1*V2 the inner product.
• Some operations will give error-messages, such as number + vector or vectorˆnumber.
• You can change an expression by using the settings-dialog of the context menu. As a result the ordering of objects in the list might change.
• You can generate a point from an expression if the result of the expression is a vector. This vector is used as the position vector for the point. You cannot define a vector from a term, because you would need to know where to draw that vector, even if you can freely translate it in theory! If you want to generate a vector from an expression, construct a free point first (named P in the following) and enter ’v=Vector(Expr,P)’, where expr is the desired expression. In case ’expr’ is a single expression-object you will have to put it into brackets to make it possible to be distinguished from a point.
• The values ’pi’ and ’e’ are defined as well as the functions sin, cos, abs (absolute value), tan, asin, acos, atan and sqrt (square root). With the exception of abs, all functions are defined for numbers only.

  For vectors, the functions x(), y() and z() are defined. The result is the corresponding co-ordinate of the vector.

  The function ’vec’ generates a vector and takes three arguments. For example, ’vec(1,2,3)’ gives the vector 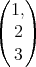, whereas ’vec(x,y,z) gives the vector with co-ordinates x, y, and z (which must be defined elsewhere, with a slider, for instance).

  While the computation of expressions is fast enough to generate surfaces from them, they are evaluated slower than geometric constructions. Wherever possible you should construct objects instead of using expressions.

  On a modern computer, a locus that is generated from an expression stays interactive with up to 40x40 supporting points⁶ You should use higher numbers of supporting points for surfaces you do not need to modify anymore. See ’HeightFieldWithParameters.geosave’ for an example.