18.2 Analytical Geometry
The following exercise is cited from a German textbook.
The plane E and the set of planes gp mit p 
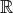 are given.
are given.

- Find an equation of the sphere with midpoint P(2|1|2) that has E as tangent-plane.
Compute the point where E touches the shpere.
- Show that gp lies in E for all values of p.
- Which lines are tangents of the sphere from part a)?
18.2.1 Solution with Archimedes
-
- Enter the plane via ’Typical tasks - Plane - General form’. One has to know that the
given normal form is the same as x + 2y + 2z = 18.
- Enter the point by double-right-clicking into the scene an setting the co-ordinates
afterwards.
- Drop the perpendicular from P to E, name the perpendicular L.
- Measure the distance from P to L. You can draw a vector or use the Macro ’Distance
- PointPoint’.
- Draw the sphere around P through L.
The sphere has the equation  2 =
2 =  2.
2.
- The claim can, of course, only be verified, not proven with Archimedes.
- Generate a slider via ’Extras - Slider’, name it ’pp’ (as the name P is already used,
there mustn’t be a second object of that name, even if you use the lowercase letter).
- Enter the equation of the line at ’Typical tasks - Line in parametric form’ with
the parameter pp like it is written in the exercise. Replace ’p’ with ’pp’. Select the
checkbox ’Expression contains terms’.
- If you change the value of pp with the slider you will see that the line moves within
E.
- We can find out by trying that the solution for the parameter p is 2, or we could construct the
line (as the parameter is not asked for) and find out the equation by right click -
description.

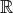 are given.
are given.

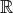 are given.
are given.

 2 =
2 =  2.
2.
