18.1 Die Inkugel eines Tetraeders

Bekanntlich ist im 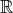² der Schnittpunkt der Winkelhalbierenden eines Dreiecks der Mittelpunkt des sogenannten Inkreises. Das ist der Kreis, der alle drei Seiten des Dreiecks als Tangenten hat.

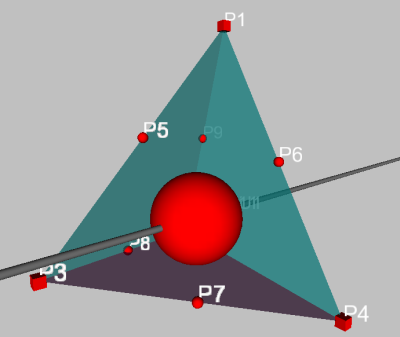
Eine analoge Konstruktion gibt es auch im 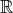³: Hier lässt sich die Inkugel eines (unregelmäßigen) Tetraeders konstruieren.

Durch Analogieschluss überlegt man sich, dass der Schnittpunkt dreier winkelhalbierender Ebenen der Mittelpunkt der Inkugel sein muss. Mit „winkelhalbierender Ebene“ ist dabei diejenige Ebene gemeint, die den Winkel zwischen zwei Tetraederseiten exakt halbiert.

Der erste Schritt einer solchen Inkugelkonstruktion sollte also das Erstellen eines Makros für winkelhalbierende Ebenen sein.

Leider ist es nicht möglich, mit zwei gegebenen Ebenen ein sinnvolles Makro „Winkelhalbierende“ zu konstruieren, da es dann Zufall ist, welche der beiden Winkelhalbierenden das Makro konstruiert. Man muss also irgendwie dem Makro die Orientierung der Zeichnung mitteilen.

Dies erreicht man, indem man statt direkt zwei Ebenen anzugeben, fünf Punkte angibt: Zwei Punkte auf der ersten Ebene, einen gemeinsamen Punkt beider Ebenen, und zwei Punkte auf der zweiten Ebene.

18.1.1 Das Winkelhalbierenden-Makro

Wer das vorhandene Makro Winkelhalbierende verwenden möchte, kann diesen Abschnitt überspringen.

Ich habe die folgende Konstruktion verwendet. Es seien P1, P2, P3, P4 und P5 freie Punkte. Dabei soll dann die eine Ebene durch P1, P2 und P3 gehen, die andere durch P3, P4 und P5. Ferner soll die erste Ebene „links“ und die zweite „rechts“ liegen, und P1 unterhalb von P2 sowie P4 unterhalb von P5.

Dadurch ist beim späteren Aufrufen des Makros sichergestellt, dass wenn der Nutzer des Makros sich an diese Orientierung hält, er auch die gewünschte Winkelhalbierende bekommt, und nicht die andere.

Des weiteren sollte das Makro möglichst „stabil“ sein. Zunächst benötigen wir die beiden Ebenen und die Schnittgerade:

• Konstruiere E1 durch P1, P2, P3
• Konstruiere E2 durch P3, P4, P5
• Konstruiere G1 als Schnitt von E1 und E2

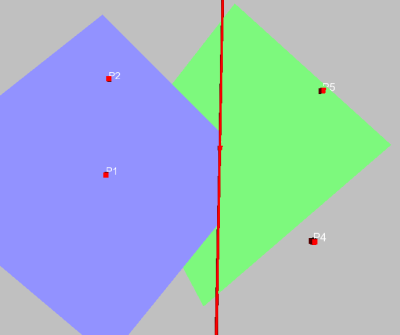
Nun benötigen wir einen Punkt, der genau zwischen den beiden Ebenen liegt, also auf der gesuchten Winkelhalbierenden. Dazu braucht man eigentlich einen Kreis mit beliebigem Radius und Mittelpunkt irgendwo auf der Schnittgeraden. Damit die Darstellung der Ebene dann aber nicht „irgendwo“ landet, nehmen wir P3, der ja auf der Geraden liegt, als Mittelpunkt, und P1 als Randpunkt des Kreises. Als Kreisebene nehmen wir die Ebene durch P3 senkrecht zu G1.

Nun muss man folgendes tun:

• Die Schnittpunkte des Kreises mit den beiden Ebenen bestimmen (z.B. mit dem Schnittbutton)
• Den Mittelpunkt der beiden Schnittpunkte konstruieren (beide Punkte markieren, dann auf Punkt drücken)
• Jetzt fehlt noch ein weiterer Punkt auf der Ebene. Dieser könnte z.B. ein beliebiger Punkt auf der Geraden G1 sein. Da ein beliebiger Punkt aber irgendwo liegen könnte - z.B. sehr in der Nähe von P3 - könnte die Ebene „instabil werden“. Also ist es besser, einen Punkt zu konstruieren, der sicherlich nicht auf P3 liegt. Dazu konstruiert man eine Kugel um P3 mit Radius P1P4 (hier gäbe es natürlich auch andere Möglichkeiten).
• Jetzt kann man die winkelhalbierende Ebene durch drei Punkte zeichnen.

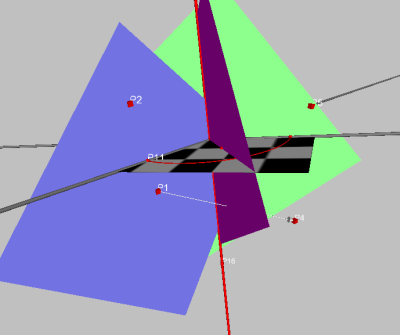
Nun sollte man mal kräftig an allen Basispunkten ziehen um zu sehen, ob die Winkelhalbierende auch „stabil“ ist.

Ferner kann man ausprobieren, was passiert, wenn P1 nicht unterhalb, sondern oberhalb von P2 liegt: Dann wandert die Winkelhalbierende „nach hinten“, da man die Orientierung der Konstruktion umgedreht hat.

Abschließend sollte man nun alle unnötigen Objekte (also alle außer der Winkelhalbierenden selbst!) verstecken, P1 bis P5 als gegeben markieren und die Konstruktion speichern, z.B. unter dem Namen „MakroWinkelhalbierendeAus5Punkten.geosave“.

18.1.2 Konstruktion der Inkugel

Nun beginnt man eine neue Zeichnung und konstruiert zuerst ein unregelmäßiges Tetraeder: Einfach vier freie Punkte konstruieren und (für die Optik) die Seitenflächen als Dreiecke.

Wenn man nun das Makro verwenden möchte, gibt es ein Problem: je zwei Seitenflächen haben nicht nur einen, sondern zwei Punkte gemeinsam, so dass man nicht die nötigen fünf Punkte für den Makroaufruf zusammen bekommt. ⁷

Hier kann man sich so behelfen, dass man noch die Mittelpunkte der Seiten konstruiert:

Markiert man nun die richtigen Punkte in der richtigen Reihenfolge, so erhält man die erste Winkelhalbierende:

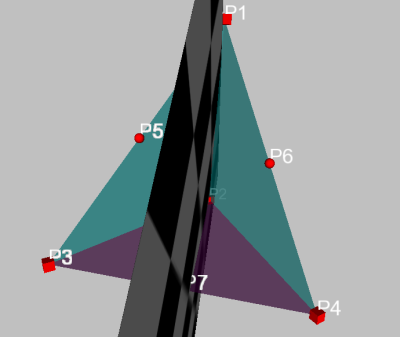
Jetzt muss man nur noch drei weitere Winkelhalbierende konstruieren und dann alle drei markieren, um den Schnittpunkt zu erhalten. Dann fällt man das Lot von diesem Schnittpunkt auf eine der Dreiecksseiten (z.B. durch Markieren des Punktes und des Dreiecks und Drücken des Normalenbuttons im kleinen Toolbar) und hat nun Mittel- und Randpunkt der Inkugel: