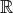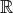10.2 Locus surfaces in ³

The generalization of loci in 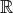² - which can be described as algebraic curves mostly - are locus surfaces in 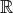³, which are algebraic surfaces as long as you only use geometric constructions (no expressions), or locus lines, which are also called geometric curves. Let’s have a look at the surfaces first:

10.2.1 Tracing a point on a plane

The easiest way to construct a locus surface is to trace a point on a plane. As an example we use the generalization of the aforementioned parabola in space: Given a plane PL1 (directrix-pane) and a point P1 (focus) the set of points P_x that have equal distance to P1 and PL1 searched for.

This can be constructed as follows:

• Construct a point P5 on PL1
• Construct the perpendicular bisector plane between P5 and P1 (select the points, press ’Point’ to get the midpoint, draw the line through P5 and P1 and construct the plane by point and normal)
• Construct the normal l1 to PL1 through P5
• Let X be the intersection of l1 and PL2.

Now you can first select P5 and then the intersection X. Press the locus-symbol (or use Alt - O), and a paraboloid appears almost immediately.

The paraboloid is dynamic, meaning that it will change if you move one of the base objects.

10.2.2 Trace a point that depends on two base points on lines, segments or circles

To get a surface, the movement that drives it must be two-dimensional. This can be the movement of a point on a plane, but you can also use two points that lay on different linear objects. A nice example using this approach is the construction of the hyperbolic paraboloid. The hyperbolic paraboloid is the set of points P_x that have equal distance to two given lines. If you need inspiration on how to construct this, have a look at the examples-folder.

In general: A locus surface is given by the selection of a point on a linear object (line, segment, circle), a second point on a linear object and a point that depends upon the first two.

10.2.3 Tracing a circle, line or segment that depends on a point on a linear object

You can trace a circle in order to generate solids with rotational symmetries. Select a point on a linear object and a circle that depends on the point. Pressing the locus-button results in a locus surface.

Using this approach you can construct the hyperboloid of two sheeds.

It is constructed analogously to constructing a hyperbola in 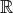². Constructing an ellipsoid is analogous to constructing an ellipse in the plane.

By tracing lines you can construct ruled surfaces.